I teach half of an integrated math & science modeling class. On the math side, we focus on functions and a little bit of right triangle trigonometry. The science side is all about motion, one dimensional and two dimensional – hence the trigonometry. We’re now entering the final few days of the trimester, and have gotten into that 2D motion part. Did I mention that this is the introductory math/science class for 9th graders at Baxter Academy?
We started with Dan Meyer‘s Will It Hit the Hoop? concept, slightly modified. Showed Act 1 video, but captured this picture for analysis.

Interesting conversation begins. Many students are convinced that the ball will fall short of the hoop because “it is slowing down.” What makes them think that, I wondered. Maybe because up until this point, the conversation in science has been about constant velocity motion, in one dimension. Showed Act 3 of course and those who were sure the ball would go in were vindicated. But their comments still nagged at me. Maybe they just need more experiences – this was, after all, just the first day of 2D motion.
We watched part of an episode of Mythbusters, the one where they fire a bullet and drop a bullet and have them land in the same spot at the same time. It’s really a good episode. It really helps to drive home the fact that the forward motion of the bullet has nothing to do with how much time it takes to fall to the ground. It means that horizontal and vertical motion can be thought of, and modeled, independently of each other. On the science side of things they had developed the kinematics model: 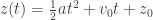 . So then we adapted that model for horizontal and vertical motion. We went back to the basketball shot. Analyzing the photo against the graph, we estimated the the initial position of the ball is at (1, 8) and the final position of the ball would be (19.75, 10). We also figured that the ball was in the air for about 1.8 seconds. From this information my students calculated the initial horizontal and initial vertical velocities to be 10.4 ft/s and 30 ft/s, respectively.
. So then we adapted that model for horizontal and vertical motion. We went back to the basketball shot. Analyzing the photo against the graph, we estimated the the initial position of the ball is at (1, 8) and the final position of the ball would be (19.75, 10). We also figured that the ball was in the air for about 1.8 seconds. From this information my students calculated the initial horizontal and initial vertical velocities to be 10.4 ft/s and 30 ft/s, respectively.

But Dan did not throw the ball only horizontally or only vertically. He threw it at an angle – so that it could reach the hoop, presumably. So I asked the question: “What was the launch velocity of the basketball?” and accompanied the question with this image:

Class was over, so I left them to work that out for homework.
Next day, I had them check in with each other and then asked, “How did you think about this problem?” Overwhelmingly, they agreed that the launch velocity must be the average of the horizontal and vertical velocities. This happened with both groups. I asked them why they thought it should be the average. I asked if they thought the launch velocity should be greater than 30 ft/s, between 10.4 ft/s and 30 ft/s, or less than 10.4 ft/s. They were convinced that the launch velocity should be somewhere between 10.4 ft/s and 30 ft/s. Some thought that it should be closer to 30 ft/s since the ball is “going more up than over,” but that it would still be less than 30 ft/s.
A student in one of the classes convinced that group that it couldn’t be the average with the following reasoning: Suppose that the ball was thrown straight up. That means that the vertical velocity is 30 ft/s and the horizontal velocity is 0 ft/s. If the launch velocity is the average, then that would be 15 ft/s, but we know that the launch velocity is 30 ft/s. So it can’t be the average! So, of course I asked, “Then what could it be?” And they went with the idea that it must be the sum of the two velocities. But that would give us a launch velocity greater than 30 ft/s. We talked about this for a few minutes. They weren’t sure.
Then I showed them this picture:

Only after seeing this picture did they make any connection to a right triangle, or Pythagorean Theorem, or trigonometry. It had taken the better part of an hour to arrive at this conclusion, and then it took only 5 minutes to find the solution.
What would have happened if I had jumped directly to the right triangle representation? They would have had a quick solution, but they wouldn’t have had the opportunity to think about whether or not the launch velocity is the average of the horizontal and vertical. Maybe you think it was a waste of class time to allow my students to engage in such discussion. Maybe it was, but I don’t think so. My students had to take some time to construct meaning. They had to confront their misconception and convince themselves and each other that taking the average didn’t make sense. Sure, I could have told them, it would have been more efficient, but would that really have helped their understanding?









